第 11 章. 数字
JavaScript 对所有数字使用单一类型:它将所有数字都视为浮点数。 但是,如果小数点后没有数字,则不显示点:
> 5.000 5
在内部,大多数 JavaScript 引擎都进行了优化,并区分了浮点数和整数(详情请参阅:JavaScript 中的整数)。 但这是程序员看不到的。
JavaScript 数字是基于 IEEE 浮点算术标准(IEEE 754)的 双精度(64 位)值。 该标准被许多编程语言使用。
数字字面量
数字字面量可以是整数、浮点数或(整数)十六进制数:
> 35 // integer 35 > 3.141 // floating point 3.141 > 0xFF // hexadecimal 255
调用字面量上的方法
对于数字字面量,用于访问属性的点必须与小数点区分开来。如果要对数字字面量 123 调用 toString(),则可以使用以下选项:
123..toString()123.toString()// space before the dot123.0.toString()(123).toString()
转换为数字
值的转换规则如下:
| 值 | 结果 |
|
|
|
|
布尔值 |
|
| |
数字 | 与输入相同(无需转换) |
字符串 | 解析字符串中的数字(忽略开头和结尾的空格);空字符串转换为 0。例如: |
对象 | 调用 |
将空字符串转换为数字时,NaN 可以说是更好的结果。 选择结果 0 是为了帮助处理空的数字输入字段,这与其他编程语言在 20 世纪 90 年代中期所做的一致。[14]
手动转换为数字
| (作为函数调用,而不是作为构造函数) |
|
我更喜欢 Number(),因为它更具描述性。以下是一些示例
> Number('')
0
> Number('123')
123
> Number('\t\v\r12.34\n ') // ignores leading and trailing whitespace
12.34
> Number(false)
0
> Number(true)
1parseFloat()
全局函数 parseFloat() 提供了另一种将值转换为数字的方法。但是,Number() 通常是更好的选择,我们稍后会看到。此代码:
parseFloat(str)
将 str 转换为字符串,删除开头空格,然后解析最长的浮点数前缀。 如果不存在此类前缀(例如,在空字符串中),则返回 NaN。
比较 parseFloat() 和 Number()
将
parseFloat()应用于非字符串效率较低,因为它在解析参数之前会将其强制转换为字符串。因此,许多Number()转换为实际数字的值会被parseFloat()转换为NaN> parseFloat(true) // same as parseFloat('true') NaN > Number(true) 1 > parseFloat(null) // same as parseFloat('null') NaN > Number(null) 0parseFloat()将空字符串解析为NaN> parseFloat('') NaN > Number('') 0parseFloat()会一直解析到最后一个合法字符,这意味着您可能会得到不需要的结果> parseFloat('123.45#') 123.45 > Number('123.45#') NaNparseFloat()忽略开头空格并在非法字符(包括空格)之前停止> parseFloat('\t\v\r12.34\n ') 12.34Number()忽略开头和结尾的空格(但其他非法字符会导致NaN)。
特殊数字值
JavaScript 有几个特殊数字值:
- 两个错误值,
NaN和Infinity。 - 两个零值,
+0和-0。JavaScript 有两个零,正零和负零,因为数字的符号和大小是分开存储的。在本书的大部分内容中,我都假装只有一个零,而且您几乎从未在 JavaScript 中看到过有两个零。
NaN
错误值 NaN(“非数字”的缩写)具有讽刺意味,它是一个数字值:
> typeof NaN 'number'
它是由以下错误产生的
无法解析数字
> Number('xyz') NaN > Number(undefined) NaN操作失败
> Math.acos(2) NaN > Math.log(-1) NaN > Math.sqrt(-1) NaN
其中一个操作数是
NaN(这可以确保如果在较长的计算过程中发生错误,您可以在最终结果中看到它)> NaN + 3 NaN > 25 / NaN NaN
陷阱:检查值是否为 NaN
NaN 是唯一不等于自身的值:
> NaN === NaN false
Array.prototype.indexOf 也使用严格相等(===)。因此,您无法通过该方法在数组中搜索 NaN
> [ NaN ].indexOf(NaN) -1
如果要检查值是否为 NaN,则必须使用全局函数 isNaN():
> isNaN(NaN) true > isNaN(33) false
但是,isNaN 对非数字不起作用,因为它首先将这些值转换为数字。该转换可能会产生 NaN,然后函数会错误地返回 true
> isNaN('xyz')
true因此,最好将 isNaN 与类型检查结合使用:
functionmyIsNaN(value){returntypeofvalue==='number'&&isNaN(value);}
或者,您可以检查该值是否不等于自身(因为 NaN 是唯一具有此特征的值)。但这不太容易理解:
functionmyIsNaN(value){returnvalue!==value;}
请注意,此行为由 IEEE 754 规定。如第 7.11 节“比较谓词的详细信息”中所述:[15]
每个 NaN 都应与所有内容进行无序比较,包括自身。
Infinity
Infinity 是一个错误值,表示以下两种问题之一:数字无法表示,因为其幅度太大,或者发生了除以零的情况。
Infinity 大于任何其他数字(NaN 除外)。同样,-Infinity 小于任何其他数字(NaN 除外)。这使得它们可以用作默认值,例如,当您要查找最小值或最大值时。
错误:数字的幅度太大
数字的幅度可以达到多大取决于其内部表示形式(如 数字的内部表示形式中所述),它是以下各项的算术乘积
- 尾数(二进制数 1.f1f2...)
- 2 的指数次幂
指数必须介于(不包括)−1023 和 1024 之间。如果指数太小,则该数字变为 0。如果指数太大,则变为 Infinity。21023 仍然可以表示,但 21024 不能
> Math.pow(2, 1023) 8.98846567431158e+307 > Math.pow(2, 1024) Infinity
使用 Infinity 进行计算
如果您尝试用另一个 Infinity“抵消”一个 Infinity,则会得到错误结果 NaN:
> Infinity - Infinity NaN > Infinity / Infinity NaN
如果您尝试超出 Infinity,您仍然会得到 Infinity
> Infinity + Infinity Infinity > Infinity * Infinity Infinity
检查 Infinity
严格相等和宽松相等对 Infinity 有效:
> var x = Infinity; > x === Infinity true
此外,全局函数 isFinite() 允许您检查值是否为实际数字(既不是无限大也不是 NaN):
> isFinite(5) true > isFinite(Infinity) false > isFinite(NaN) false
两个零
因为 JavaScript 的数字将大小和符号分开保存,所以每个非负数都有一个负数,包括 0。
这样做的理由是,每当您以数字形式表示数字时,它都可能变得非常小,以至于无法与 0 区分开来,因为编码不够精确,无法表示差异。然后,带符号的零允许您记录您接近零的“方向”;也就是说,数字在被视为零之前的符号。维基百科很好地总结了带符号的零的优缺点
据称,在 IEEE 754 中包含带符号的零使得在某些关键问题中更容易实现数值精度,特别是在使用复数基本函数进行计算时。另一方面,带符号的零的概念与大多数数学领域(以及大多数数学课程)中的一般假设背道而驰,即负零与零相同。允许负零的表示形式可能会成为程序中错误的根源,因为软件开发人员没有意识到(或者可能忘记了),虽然这两种零表示形式在数值比较下表现相同,但它们是不同的位模式,并且在某些操作中会产生不同的结果。
最佳实践:假装只有一个零
JavaScript 想方设法隐藏了有两个零的事实。鉴于它们通常没有区别,因此建议您配合单一零的错觉。让我们看看这种错觉是如何维持的。
在 JavaScript 中,您通常编写 0,这意味着 +0。但是 -0 也显示为 0。这是您在使用浏览器命令行或 Node.js REPL 时看到的内容
> -0 0
这是因为标准的 toString() 方法将两个零都转换为相同的 '0':
> (-0).toString() '0' > (+0).toString() '0'
相等性也不区分零。即使是 === 也不行:
> +0 === -0 true
Array.prototype.indexOf 使用 === 来搜索元素,从而保持了这种错觉
> [ -0, +0 ].indexOf(+0) 0 > [ +0, -0 ].indexOf(-0) 0
排序运算符也认为零是相等的
> -0 < +0 false > +0 < -0 false
区分两个零
您如何实际观察到两个零是不同的?您可以除以零(-Infinity 和 +Infinity 可以 通过 === 区分):
> 3 / -0 -Infinity > 3 / +0 Infinity
另一种执行除以零的方法是通过 Math.pow()(请参阅 数值函数)
> Math.pow(-0, -1) -Infinity > Math.pow(+0, -1) Infinity
Math.atan2()(请参阅 三角函数)也表明这两个零是不同的:
> Math.atan2(-0, -1) -3.141592653589793 > Math.atan2(+0, -1) 3.141592653589793
区分这两个零的规范方法是除以零。因此,用于检测负零的函数看起来如下所示:
functionisNegativeZero(x){returnx===0&&(1/x<0);}
以下是该函数的使用方法
> isNegativeZero(0) false > isNegativeZero(-0) true > isNegativeZero(33) false
数字的内部表示形式
JavaScript 数字具有 64 位精度,也称为双精度(在某些编程语言中为 double 类型)。 内部表示形式基于 IEEE 754 标准。64 位分布在数字的符号、指数和小数部分之间,如下所示:
| 符号 | 指数 ∈ [−1023, 1024] | 小数部分 |
1 位 | 11 位 | 52 位 |
第 63 位 | 第 62–52 位 | 第 51–0 位 |
数字的值由以下公式计算得出
(–1)符号 × %1.分数 × 2指数
前缀百分号 (%) 表示中间的数字以二进制表示法编写:一个 1,后跟一个二进制小数点,再后跟一个二进制分数,即分数(自然数)的二进制数字。 以下是此表示法的一些示例:
+0 | (符号 = 0,分数 = 0,指数 = −1023) | |
–0 | (符号 = 1,分数 = 0,指数 = −1023) | |
1 | = (−1)0 × %1.0 × 20 | (符号 = 0,分数 = 0,指数 = 0) |
2 | = (−1)0 × %1.0 × 21 | |
3 | = (−1)0 × %1.1 × 21 | (符号 = 0,分数 = 251,指数 = 0) |
0.5 | = (−1)0 × %1.0 × 2−1 | |
−1 | = (−1)1 × %1.0 × 20 |
+0、−0 和 3 的编码可以解释如下
- ±0:鉴于分数始终以 1 为前缀,因此无法用它表示 0。因此,JavaScript 通过分数 0 和特殊指数 −1023 对零进行编码。符号可以是正数也可以是负数,这意味着 JavaScript 有两个零(请参阅两个零)。
- 3:第 51 位是分数的最高有效位。该位为 1。
特殊指数
前面提到的数字表示法 称为 规范化。 在这种情况下,指数 e 的范围为 −1023 < e < 1024(不包括下限和上限)。−1023 和 1024 是特殊指数:
- 1024 用于错误值,例如
NaN和Infinity。 −1023 用于
- 零(如果分数为 0,如前所述)
- 接近零的小数(如果分数不为 0)。
为了同时启用这两种应用,使用了不同的、所谓的 非规范化 表示法:
(–1)符号 × %0.分数 × 2–1022
为了进行比较,规范化表示法中最小的(即“最接近零”)数字是
(–1)符号 × %1.分数 × 2–1022
非规范化数字更小,因为没有前导数字 1。
处理舍入误差
JavaScript 的数字通常以十进制浮点数输入,但它们在内部表示为二进制浮点数。 这会导致不精确。为了理解原因,让我们忘记 JavaScript 的内部存储格式,并总体看一下哪些分数可以用十进制浮点数和二进制浮点数很好地表示。在十进制系统中,所有分数都是尾数 m 除以 10 的幂:
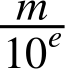
因此,在分母中,只有十。这就是为什么 ![]() 不能精确地表示为十进制浮点数的原因,因为无法在分母中得到 3。二进制浮点数在分母中只有 2。让我们检查一下哪些十进制浮点数可以很好地表示为二进制数,哪些不能。如果分母中只有 2,则可以表示十进制数
不能精确地表示为十进制浮点数的原因,因为无法在分母中得到 3。二进制浮点数在分母中只有 2。让我们检查一下哪些十进制浮点数可以很好地表示为二进制数,哪些不能。如果分母中只有 2,则可以表示十进制数
- 0.5dec =
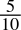 =
= 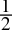 = 0.1bin
= 0.1bin - 0.75dec =
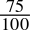 =
= 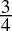 = 0.11bin
= 0.11bin - 0.125dec =
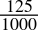 =
= 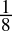 = 0.001bin
= 0.001bin
其他分数不能精确表示,因为它们在分母中(在质因数分解后)有除 2 以外的数字
- 0.1dec =
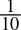 =
= 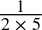
- 0.2dec =
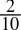 =
= 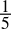
您通常看不到 JavaScript 在内部没有精确存储 0.1。但是,您可以通过将其乘以足够高的 10 的幂来使其可见
> 0.1 * Math.pow(10, 24) 1.0000000000000001e+23
而且,如果将两个不精确表示的数字相加,结果有时会不精确到足以使不精确性变得可见
> 0.1 + 0.2 0.30000000000000004
另一个例子
> 0.1 + 1 - 1 0.10000000000000009
由于舍入误差,最佳做法是不应直接比较非整数。相反,应考虑舍入误差的上限。这样的上限称为 机器ε。双精度的标准 ε 值为 2−53:
varEPSILON=Math.pow(2,-53);functionepsEqu(x,y){returnMath.abs(x-y)<EPSILON;}
epsEqu() 可确保在正常比较不充分的情况下获得正确的结果
> 0.1 + 0.2 === 0.3 false > epsEqu(0.1+0.2, 0.3) true
JavaScript 中的整数
如前所述,JavaScript 只有浮点数。 整数在内部以两种方式出现。首先,大多数 JavaScript 引擎将一个没有小数部分且足够小的数字存储为整数(例如,使用 31 位),并在尽可能长的时间内保持该表示形式。如果数字的大小变得太大或出现小数部分,则它们必须切换回浮点表示形式。
其次,ECMAScript 规范具有整数运算符:即所有按位运算符。 这些运算符将其操作数转换为 32 位整数,并 返回 32 位整数。对于规范,整数 仅表示数字没有小数部分,而 32 位 表示它们在一定范围内。对于引擎,32 位整数 表示通常可以引入或维护实际的整数(非浮点)表示形式。
将整数表示为浮点数
JavaScript 只能处理最大为 53 位的整数值(分数的 52 位加上 1 个间接位,通过指数;有关详细信息,请参阅数字的内部表示)。
下表说明了 JavaScript 如何将 53 位整数表示为浮点数
| 位 | 范围 | 编码 |
1 位 | 0 | (请参阅数字的内部表示。) |
1 位 | 1 | %1 × 20 |
2 位 | 2–3 | %1.f51 × 21 |
3 位 | 4–7 = 22–(23−1) | %1.f51f50 × 22 |
4 位 | 23–(24−1) | %1.f51f50f49 × 23 |
⋯ | ⋯ | ⋯ |
53 位 | 252–(253−1) | %1.f51⋯f0 × 252 |
没有固定的位序列来表示整数。相反,尾数 %1.f 由指数移位,以便前导数字 1 位于正确的位置。在某种程度上,指数计算的是正在使用的分数的位数(其余位为 0)。这意味着对于 2 位,我们使用分数的一位数字,而对于 53 位,我们使用分数的所有数字。此外,我们可以将 253 表示为 %1.0 × 253,但是对于更大的数字,我们会遇到问题
| 位 | 范围 | 编码 |
54 位 | 253–(254−1) | %1.f51⋯f00 × 253 |
55 位 | 254–(255−1) | %1.f51⋯f000 × 254 |
⋯ |
对于 54 位,最低有效位始终为 0,对于 55 位,两个最低有效位始终为 0,依此类推。这意味着对于 54 位,我们只能表示每隔一个数字,对于 55 位,只能表示每隔四个数字,依此类推。例如
> Math.pow(2, 53) - 1 // OK 9007199254740991 > Math.pow(2, 53) // OK 9007199254740992 > Math.pow(2, 53) + 1 // can't be represented 9007199254740992 > Math.pow(2, 53) + 2 // OK 9007199254740994
安全整数
JavaScript 只能安全地表示范围为 −253 < i < 253 的整数 i。 本节将检查这意味着什么以及后果是什么。它基于Mark S. Miller 发送给 es-discuss 邮件列表的电子邮件。
安全整数的概念集中于如何在 JavaScript 中表示数学整数。在 (−253, 253) 范围内(不包括下限和上限),JavaScript 整数是 安全的:数学整数与其在 JavaScript 中的表示形式之间存在一对一的映射。
超出此范围,JavaScript 整数是 不安全的:两个或多个数学整数表示为相同的 JavaScript 整数。例如,从 253 开始,JavaScript 只能表示每隔一个数学整数(上一节解释了原因)。因此,安全的 JavaScript 整数是明确表示单个数学整数的整数。
ECMAScript 6 中的定义
ECMAScript 6 将 提供以下常量:
Number.MAX_SAFE_INTEGER=Math.pow(2,53)-1;Number.MIN_SAFE_INTEGER=-Number.MAX_SAFE_INTEGER;
它还将提供一个函数来确定 整数是否安全:
Number.isSafeInteger=function(n){return(typeofn==='number'&&Math.round(n)===n&&Number.MIN_SAFE_INTEGER<=n&&n<=Number.MAX_SAFE_INTEGER);}
对于给定值 n,此函数首先检查 n 是否为数字和整数。如果两项检查均成功,则如果 n 大于或等于 MIN_SAFE_INTEGER 且小于或等于 MAX_SAFE_INTEGER,则 n 是安全的。
算术计算的安全结果
我们如何确保算术 计算的结果是正确的?例如,以下结果显然是不正确的:
> 9007199254740990 + 3 9007199254740992
我们有两个安全的操作数,但结果不安全
> Number.isSafeInteger(9007199254740990) true > Number.isSafeInteger(3) true > Number.isSafeInteger(9007199254740992) false
以下结果也不正确
> 9007199254740995 - 10 9007199254740986
这次,结果是安全的,但其中一个操作数不是
> Number.isSafeInteger(9007199254740995) false > Number.isSafeInteger(10) true > Number.isSafeInteger(9007199254740986) true
因此,仅当所有操作数和结果均安全时,应用整数运算符 op 的结果才能保证是正确的。更正式地说
isSafeInteger(a) && isSafeInteger(b) && isSafeInteger(a op b)
意味着 a op b 是正确的结果。
转换为整数
在 JavaScript 中,所有数字都是浮点数。 整数是没有小数部分的浮点数。将数字 n 转换为整数意味着找到“最接近”n 的整数(“最接近”的含义取决于转换方式)。您可以通过以下几种方式执行此转换:
Math函数Math.floor()、Math.ceil()和Math.round()(请参阅 通过 Math.floor()、Math.ceil() 和 Math.round() 获取整数)- 自定义函数
ToInteger()(请参阅 通过自定义函数 ToInteger() 获取整数) - 二进制位运算符(请参阅 通过位运算符获取 32 位整数)
- 全局函数
parseInt()(请参阅 通过 parseInt() 获取整数)
剧透:#1 通常是最佳选择,#2 和 #3 适用于特定情况,#4 适用于解析字符串,但不适用于将数字转换为整数。
通过 Math.floor()、Math.ceil() 和 Math.round() 获取整数
以下三个函数通常是将数字转换为整数的最佳方式
Math.floor()将其参数转换为 最接近的较小整数:> Math.floor(3.8) 3 > Math.floor(-3.8) -4
Math.ceil()将其参数转换为 最接近的较大整数:> Math.ceil(3.2) 4 > Math.ceil(-3.2) -3
Math.round()将其参数转换为 最接近的整数:> Math.round(3.2) 3 > Math.round(3.5) 4 > Math.round(3.8) 4
舍入
-3.5的结果可能会令人惊讶> Math.round(-3.2) -3 > Math.round(-3.5) -3 > Math.round(-3.8) -4
因此,
Math.round(x)等同于Math.floor(x+0.5)
通过自定义函数 ToInteger() 获取整数
将任何值转换为整数的另一个好方法是使用内部 ECMAScript 操作 ToInteger(),它会移除浮点数的小数部分。 如果它在 JavaScript 中可用,则其工作方式如下:
> ToInteger(3.2) 3 > ToInteger(3.5) 3 > ToInteger(3.8) 3 > ToInteger(-3.2) -3 > ToInteger(-3.5) -3 > ToInteger(-3.8) -3
ECMAScript 规范将 ToInteger(number) 的结果定义为
sign(number) × floor(abs(number))
就其功能而言,此公式相对复杂,因为 floor 寻找最接近的 较大 整数;如果要移除负整数的小数部分,则必须寻找最接近的较小整数。以下代码在 JavaScript 中实现了此操作。我们通过在数字为负数时使用 ceil 来避免 sign 操作
functionToInteger(x){x=Number(x);returnx<0?Math.ceil(x):Math.floor(x);}
二进制位运算符(请参阅 二进制位运算符)将其至少一个操作数转换为 32 位整数,然后对其进行操作以生成同样是 32 位整数的结果。 因此,如果您适当地选择另一个操作数,则可以获得一种将任意数字快速转换为 32 位整数(有符号或无符号)的方法。
按位或 (|)
如果掩码(第二个操作数)为 0,则不会更改任何位,并且结果是第一个操作数,强制转换为有符号 32 位整数。 这是执行此类强制转换的规范方法,例如,asm.js 使用了此方法(请参阅 JavaScript 是否足够快?)
// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx|0;}
ToInt32() 移除 小数部分并应用模 232:
> ToInt32(1.001) 1 > ToInt32(1.999) 1 > ToInt32(1) 1 > ToInt32(-1) -1 > ToInt32(Math.pow(2, 32)+1) 1 > ToInt32(Math.pow(2, 32)-1) -1
移位运算符
适用于按位或的技巧也适用于移位运算符:如果移位 0 位,则移位操作的结果是第一个操作数,强制转换为 32 位整数。 以下是一些通过移位运算符实现 ECMAScript 规范操作的示例:
// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx<<0;}// Convert x to a signed 32-bit integerfunctionToInt32(x){returnx>>0;}// Convert x to an unsigned 32-bit integerfunctionToUint32(x){returnx>>>0;}
以下是 ToUint32() 在 实际应用中的示例:
> ToUint32(-1) 4294967295 > ToUint32(Math.pow(2, 32)-1) 4294967295 > ToUint32(Math.pow(2, 32)) 0
我应该使用位运算符来强制转换为整数吗?
您必须自行决定效率的略微提高 是否值得以代码更难理解为代价。另请注意,位运算符人为地将自己限制为 32 位,这通常既不必要也不有用。使用 Math 函数之一(可能还需要 Math.abs())是一种更易于理解且可以说是更好的选择。
通过 parseInt() 获取整数
parseInt() 函数:
parseInt(str,radix?)
将字符串 str(非字符串将被强制转换)解析为整数。该函数会忽略前导空格,并尽可能多地考虑连续的合法数字。
基数
基数的范围为 2 ≤ radix ≤ 36。它决定了要解析的数字的基数。如果基数大于 10,则除了 0-9 之外,还会使用字母作为数字(不区分大小写)。
如果缺少 radix,则假定为 10,除非 str 以“0x”或“0X”开头,在这种情况下,radix 设置为 16(十六进制)
> parseInt('0xA')
10如果 radix 已经是 16,则十六进制前缀是可选的
> parseInt('0xA', 16)
10
> parseInt('A', 16)
10到目前为止,我已经根据 ECMAScript 规范描述了 parseInt() 的行为。此外,如果 str 以零开头,则某些引擎会将基数设置为 8
> parseInt('010')
8
> parseInt('0109') // ignores digits ≥ 8
8因此,最好始终显式声明基数,始终使用两个参数调用 parseInt()。
以下是一些示例
> parseInt('')
NaN
> parseInt('zz', 36)
1295
> parseInt(' 81', 10)
81
> parseInt('12**', 10)
12
> parseInt('12.34', 10)
12
> parseInt(12.34, 10)
12不要使用 parseInt() 将数字转换为整数。最后一个示例让我们看到了可以使用 parseInt() 将数字转换为整数的希望。 唉,以下是一个转换不正确的示例:
> parseInt(1000000000000000000000.5, 10) 1
说明
参数首先转换为字符串
> String(1000000000000000000000.5) '1e+21'
parseInt 不认为“e”是整数数字,因此在 1 之后停止解析。以下是另一个示例
> parseInt(0.0000008, 10) 8 > String(0.0000008) '8e-7'
总结
不应使用 parseInt() 将数字转换为整数:强制转换为字符串是不必要的迂回操作,即使这样,结果也不总是正确的。
parseInt() 适用于 解析字符串,但您必须注意,它会在遇到第一个非法数字时停止。通过 Number() 解析字符串(请参阅 函数 Number)不太宽容,但可能会产生非整数。
算术运算符
以下运算符可用于 数字:
-
number1 + number2 数字加法,除非其中一个操作数是字符串。然后,两个操作数都将转换为字符串并连接在一起 (请参阅 加号运算符 (+))
> 3.1 + 4.3 7.4 > 4 + ' messages' '4 messages'
-
number1 - number2 - 减法。
-
number1 * number2 - 乘法。
-
number1 / number2 - 除法。
-
number1 % number2 取余
> 9 % 7 2 > -9 % 7 -2
警告
此操作不是模运算。它返回一个符号与第一个操作数相同的的值(稍后将详细介绍)。
-
-number - 对其 操作数取反。
-
+number - 保持其操作数不变;非数字将转换为数字。
-
++variable、--variable > var x = 3; > ++x 4 > x 4
-
variable++、variable-- 将变量的值加 1(或减 1),并返回其值
> var x = 3; > x++ 3 > x 4
助记符:递增 (++) 和递减 (--) 运算符
操作数的位置可以帮助您记住是在递增(或递减)之前还是之后返回它。如果操作数位于递增运算符之前,则在递增之前返回它。如果操作数位于运算符之后,则先递增它,然后再返回它。(递减运算符的工作方式类似。)
位运算符
JavaScript 具有多个使用 32 位整数的位运算符。 也就是说,它们会将其操作数转换为 32 位整数,并生成一个 32 位整数作为结果。这些运算符的用例包括处理二进制协议、特殊算法等。
背景知识
本节介绍一些有助于您理解位运算符的概念。
二进制补码
计算二进制数的二进制补码(或反码)的两种常见方法是
- 反码
您可以通过反转 32 位中的每一位来计算数字
x的反码~x。让我们用四位数字来说明反码。1100的反码是0011。将一个数字与其反码相加会得到一个所有数字均为 1 的数字1 + ~1 = 0001 + 1110 = 1111
- 补码
数字
x的补码-x是其反码加 1。将一个数字与其补码相加会得到0(忽略超出最高有效位的溢出)。以下是一个使用四位数字的示例1 + -1 = 0001 + 1111 = 0000
有符号 32 位整数
32 位整数没有显式符号,但您仍然可以对负数进行编码。 例如,−1 可以编码为 1 的补码:将 1 与结果相加得到 0(在 32 位内)。正数和负数之间的界限是模糊的;4294967295 (232−1) 和 −1 在这里是相同的整数。但是,当您将此类整数与 JavaScript 数字(具有显式符号而不是隐式符号)进行相互转换时,必须确定符号。因此,有符号 32 位整数 分为两组:
- 最高位为 0:数字为零或正数。
- 最高位为 1:数字为负数。
最高位通常称为 符号位。因此,当转换为 JavaScript 数字时,解释为有符号 32 位整数的 4294967295 变为 −1
> ToInt32(4294967295) -1
ToInt32() 在 通过位运算符获取 32 位整数 中进行了说明。
注意
只有无符号右移运算符 (>>>) 使用无符号 32 位整数;所有其他位运算符都使用有符号 32 位整数。
输入和输出二进制数
在以下示例中,我们通过以下两个操作使用二进制数:
parseInt(str, 2)(请参阅 通过 parseInt() 获取整数)以二进制表示法(基数 2)解析字符串str。 例如:> parseInt('110', 2) 6num.toString(2)(请参阅 Number.prototype.toString(radix?))将 数字num转换为二进制表示法的字符串。例如:> 6..toString(2) '110'
二进制位运算符
JavaScript 有三个二进制位运算符
有两种方法可以直观地理解二进制位运算符
- 每一位进行一次布尔运算
在以下公式中,
ni表示数字n的第i位,解释为布尔值(0 为false,1 为true)。例如,20为false;21为true- 与:
resulti = number1i && number2i - 或:
resulti = number1i || number2i 异或:
resulti = number1i ^^ number2i运算符
^^不存在。如果存在,它的工作原理如下(如果两个操作数中只有一个为true,则结果为true)x^^y===(x&&!y)||(!x&&y)
- 与:
- 通过
number2更改number1的位 - 与:仅保留
number1中在number2中设置的位。此操作也称为掩码,其中number2为掩码。 - 或:设置
number1中在number2中设置的所有位,并保持所有其他位不变。 - 异或:反转
number1中在number2中设置的所有位,并保持所有其他位不变。
- 与:仅保留
位移运算符
> (parseInt('1', 2) << 1).toString(2) '10'32 位二进制数被解释为带符号的(请参阅上一节)。右移时,符号保持不变
> (parseInt('11111111111111111111111111111110', 2) >> 1).toString(2) '-1'我们已经将 -2 右移。 结果 -1 等效于一个 32 位整数,其所有位均为 1(1 的二进制补码)。换句话说,右移一位将负整数和正整数都除以 2。
number >>> digitCount` (无符号右移)
> (parseInt('11100', 2) >>> 1).toString(2) '1110'如您所见,此运算符从左侧移入零。
Number 构造函数属性
对象 Number 具有以下属性
-
Number.MAX_VALUE 可以表示的最大正数。 在内部,其小数的所有位均为 1,指数最大为 1023。如果尝试通过将其乘以 2 来增加指数,则结果为错误值
Infinity(请参阅无穷大)> Number.MAX_VALUE 1.7976931348623157e+308 > Number.MAX_VALUE * 2 Infinity
-
Number.MIN_VALUE 可表示的最小正数(大于零,一个很小的分数):
> Number.MIN_VALUE 5e-324
-
Number.NaN - 与全局
NaN相同的值。 -
Number.NEGATIVE_INFINITY 与
-Infinity相同的值:> Number.NEGATIVE_INFINITY === -Infinity true
-
Number.POSITIVE_INFINITY 与
Infinity相同的值:> Number.POSITIVE_INFINITY === Infinity true
Number 原型方法
原始数字的所有方法都存储在 Number.prototype 中(请参阅原始值从包装器借用其方法)。
Number.prototype.toFixed(fractionDigits?)
Number.prototype.toFixed(fractionDigits?) 返回该数字的无指数表示形式,四舍五入到 fractionDigits 位。如果省略该参数,则使用值 0:
> 0.0000003.toFixed(10) '0.0000003000' > 0.0000003.toString() '3e-7'
如果该数字大于或等于 1021,则此方法的工作方式与 toString() 相同。您将获得一个指数表示法的数字
> 1234567890123456789012..toFixed() '1.2345678901234568e+21' > 1234567890123456789012..toString() '1.2345678901234568e+21'
Number.prototype.toPrecision(precision?)
Number.prototype.toPrecision(precision?) 在使用类似于 toString() 的转换算法之前,将尾数截断为 precision 位。如果没有给出精度,则直接使用 toString():
> 1234..toPrecision(3) '1.23e+3' > 1234..toPrecision(4) '1234' > 1234..toPrecision(5) '1234.0' > 1.234.toPrecision(3) '1.23'
您需要使用指数表示法以三位精度显示 1234。
Number.prototype.toString(radix?)
对于 Number.prototype.toString(radix?),参数 radix 指示要显示数字的进制。 最常见的进制是 10(十进制)、2(二进制)和 16(十六进制):
> 15..toString(2) '1111' > 65535..toString(16) 'ffff'
进制必须至少为 2,最多为 36。 任何大于 10 的进制都会导致使用字母字符作为数字,这解释了最大值为 36,因为拉丁字母表有 26 个字符:
> 1234567890..toString(36) 'kf12oi'
全局函数 parseInt(请参阅通过 parseInt() 获取整数)允许您将此类表示法转换回数字:
> parseInt('kf12oi', 36)
1234567890十进制指数表示法
对于进制 10,toString() 在两种情况下使用指数表示法(小数点前一位数字)。首先,如果一个数字的小数点前有超过 21 位数字
> 1234567890123456789012 1.2345678901234568e+21 > 123456789012345678901 123456789012345680000
其次,如果一个数字以 0. 开头,后跟五个以上的零和一个非零数字
> 0.0000003 3e-7 > 0.000003 0.000003
在所有其他情况下,都使用定点表示法。
Number.prototype.toExponential(fractionDigits?)
Number.prototype.toExponential(fractionDigits?) 强制以指数表示法表示数字。 fractionDigits 是一个介于 0 和 20 之间的数字,它决定了小数点后应该显示多少位数字。如果省略,则包含尽可能多的有效数字以唯一地指定该数字。
在此示例中,当 toString() 也使用指数表示法时,我们强制提高精度。结果是混合的,因为我们在将二进制数转换为十进制表示法时达到了可以实现的精度极限
> 1234567890123456789012..toString() '1.2345678901234568e+21' > 1234567890123456789012..toExponential(20) '1.23456789012345677414e+21'
在此示例中,数字的数量级不足以使 toString() 显示指数。但是,toExponential() 确实显示了指数
> 1234..toString() '1234' > 1234..toExponential(5) '1.23400e+3' > 1234..toExponential() '1.234e+3'
在此示例中,当分数不够小时,我们将获得指数表示法
> 0.003.toString() '0.003' > 0.003.toExponential(4) '3.0000e-3' > 0.003.toExponential() '3e-3'
数字函数
以下函数对数字进行操作:
-
isFinite(number) - 检查
number是否为实际数字(既不是Infinity也不是NaN)。有关详细信息,请参阅检查无穷大。 -
isNaN(number) - 如果
number为NaN,则返回true。有关详细信息,请参阅陷阱:检查值是否为 NaN。 -
parseFloat(str) - 将
str转换为浮点数。有关详细信息,请参阅parseFloat()。 -
parseInt(str, radix?) - 将
str解析为一个以radix(2-36)为基数的整数。有关详细信息,请参阅通过 parseInt() 获取整数。